Научный предмет диморфологии

Общая диморфологическая теория

Определение предмета дискретной морфологии. Поясняющие примеры из области механики. Диморфоз. Диморфологические гипотезы об относительности. Математические замечания.

Определение

Специальным научным предметом диморфологии (дискретной морфологии, половедения) является множество конечных структурно-функциональных свойств динамической системы.

Примеры

В качестве дидактического пособия читателю предлагаются, по порядку возрастания сложности, следующие умозрительные примеры.

Притяжение — обратный пример

Для начала, рассмотрим тривиальный случай, когда диморфологическое явление отсутствует. Воображаемый объект состоит из двух веполей [Альтшуллер Г. С.: Творчество как точная наука]: физического тела и гравитационного поля.

Сила притяжения действует на тело, поэтому оно ускоряется по направлению к источнику силы — центру массы. Сила действует на тело целиком и нельзя выделить конечную часть этого тела, специализированную на передаче телу управления притяжением. Искомой конечной сущностью является отдельное, по отношению к данному, тело. Из классической механики [Ньютон И.] известно, что модуль силы притяжения во всякой точке тела не опосредован самому телу, а зависит от массы источника притяжения и расстояния между данной точкой и центром массы источника.

Всплывание — простой пример

Рассмотрим теперь систему с наличием диморфологического явления. Принцип работы воздушного шара (стратосферы) заключается в том, что кроме притяжения к земле, на него со стороны окружающей среды также действует Архимедова сила выталкивания.

Поскольку модуль силы выталкивания зависит для каждой части объёма устройства от массы вещества, которая заключена в данном объёме, наблюдается дихотомическая дифференциация структуры и функции устройства. Один морфологический элемент (оперативная подсистема) состоит из атмосферы шара и специализируется на передаче системе из среды силы выталкивания. Другой морфологический элемент (консервативная подсистема) включает такие компоненты устройства как полезный груз, материал оболочки шара и пр., за исключением атмосферы шара. Консервативная, в аспекте способности ко всплыванию, подсистема сама всплывает незначительно, но меняет своё положение в пространстве вслед за оперативной подсистемой, с которой составляет единое физическое целое.

Руление — сложный пример

Рассмотрим более выразительный случай диморфологического явления: управление автомобилем посредством пары рулевых колёс.

Все колёса составляют с автомобилем физическое целое, способное в норме перемещаться на плоскости вперёд и назад по направлению, касательному к передне-задней оси автомобиля. Рулевые колёса дихотомически дифференцируются по отношению к остальным компонентам автомобиля, включая руль и даже водителя, в качестве оперативной подсистемы, которая передаёт целой системе направление движения.

На данном примере проанализируем исчерпывающий набор вариантов предельного развития динамической траектории при отсутствии управляющих сигналов.

• Стоянка. Автомобиль не движется и предел его траектории совпадает с текущим положением.
• Движение прямо. Автомобиль едет неопределённо далеко, когда рулевые колёса установлены прямо. Геометрический предел такой траектории измеряется бесконечностью.
• Поворот. Рулевые колёса отклонены на некоторый угол. Автомобиль движется по окружности. Предел такой траектории является точкой на этой окружности. Если поделить окружность на N равных дуг, предельная точка траектории с вероятностью 1/N будет принадлежать каждой такой дуге.
• Занос. Для этого случая характерно перемещение автомобиля по траектории, которая не соответствует ни направлению передне-задней оси, ни углу рулевых колёс. Подобное развитие в математике называется хаотическим, а в психологии — произвольным. Предел зависит от множества факторов и сложно определяется даже через вероятности.

Диморфоз

Согласно общей теории относительности [Эйнштейн А.], никакие физические взаимодействия не могут осуществляться со скоростью, превышающей скорость света в плоском вакууме (3*10^8 м/с). Закономерно, что всякая причинно-следственная цепочка событий обладает положительным по значению свойством длительности. Следовательно, конечная подсистема, специализированная на передаче системе управления, управляется раньше сама, чем система в целом.

Таким образом, динамическое развитие системы происходит не одномоментно и однородно, а асинхронно и в качестве двух дискретных подсистем: оперативной и консервативной [Геодакян В. А. Роль полов в передаче и преобразовании генетической информации // Проблемы передачи информации, 1965], форма и поведение которых на обоих временных пределах диморфоза совпадает с целой системой и дихотомически дифференцируется на промежутке.

Элементарным диморфологическим предметом является диморфоз [Пинский Д. В.], а всякое развитие динамической системы под управлением гомологического ряда доминант сущностно состоит из множества асинхронных диморфозов.

Математическое содержание диморфоза представляет собой частный случай гистерезиса (греч. ὑστέρησις — отставание, запаздывание). Данный общеупотребимый термин операционально обозначает свойство системы, мгновенный отклик которой на приложенные воздействия зависит в том числе от её текущего состояния, а поведение которой на интервале времени определяется в т. ч. её предысторией.

С целью приложения диморфоза в качестве модели объектов частных диморфологических дисциплин, в соответствии с требованием общей топологии, здесь определена абстрактная топологическая структура диморфоза.

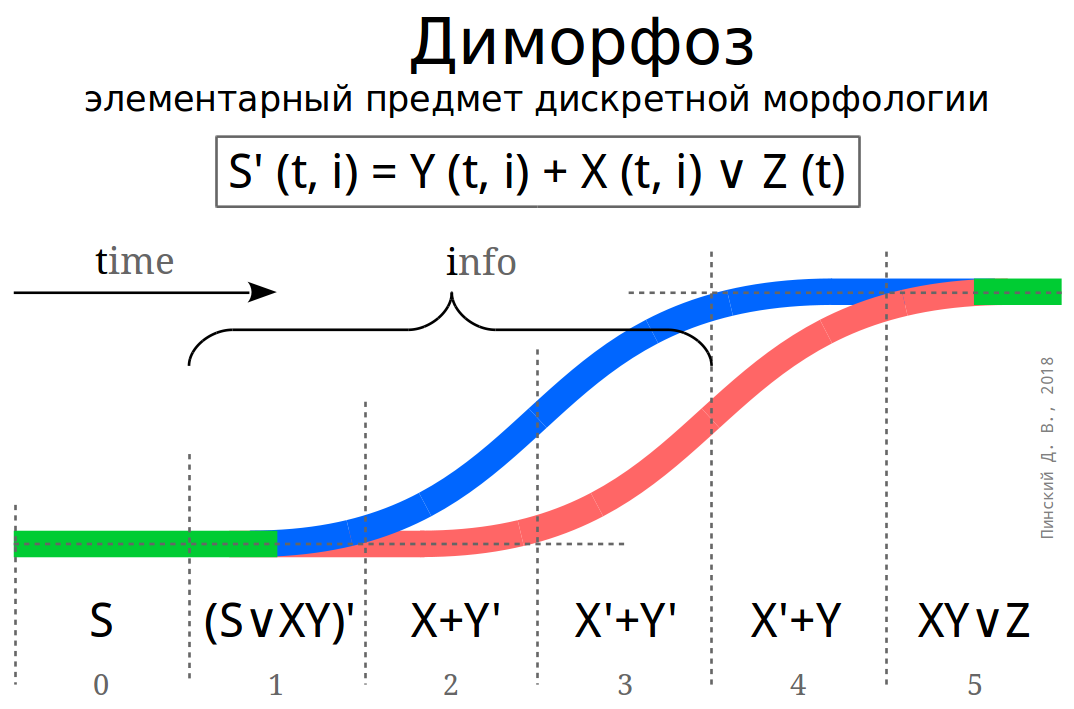
Нормальный диморфоз как физический процесс осуществляется за шесть последовательных дискретных этапов (см. Рис.), имеющих ненулевую длительность. На начальном (нулевом) этапе система представлена формой S, а на конечном (пятом) — отличной от S производной формой S' (t, i), где аргументами морфологической функции являются время и управляющая информация, при этом S' = Y (t, i) + X (t, i). Последняя формула означает соответствие формы S' слитым воедино формам дискретных подсистем, дифференцированных на промежуточных этапах диморфоза. В случае, если это условие не выполняется, имеет место явление, которое можно альтернативно назвать ненормальным диморфозом. Такой случай в формуле обозначен правым операндом дизъюнкции Z (t), явно независимым от управляющей информации. Данный поход позволяет на основании математического анализа определить участие управления в процессе развития системы: если развитие не соответствует физическому прогнозу по формуле X + Y, значит имеет место Z (“занос”), т. е. хаотическое (произвольное) вмешательство управления в нормальный процесс.

На промежуточных (с первого по пятый) этапах диморфоза система морфологически (по структуре и поведении) дифференцируется на две дискретные подсистемы. Оперативная подсистема специализируется на передаче системе управляющей информации и развивается под управлением этой информации раньше, чем консервативная подсистема и, таким образом, вся система в целом. На формулах здесь оперативная и консервативная подсистемы обозначаются, соответственно, как Y и X, по аналогии с половыми хромосомами.

Первый (следующий после нулевого) этап нормального диморфоза характеризуется латентной дифференцированностью специфических, по отношению к управляющей доминанте, подсистем. Это выражается в том, что управление уже происходит, но подсистемы ещё не являются дифференцированными на всём промежутке этапа. На формуле первый этап диморфоза обозначен как (S v XY)', что следует понимать как морфологическую производную от дизъюнкции начально слитного и дифференцированного состояний системы. Явление дивергенции (расхождения) впервые наблюдается в окрестности переходного мгновения между первым и вторым этапом диморфоза.

На втором этапе дифференциация системы наблюдается явно, при этом развитие оперативной подсистемы уже происходит с нарастающей скоростью, а до консервативной подсистемы управление ещё “не дошло”, поэтому её форма и поведение соответствует таковым в начальном состоянии системы S. На формуле второй этап диморфоза обозначен как X + Y', что подчёркивает явную дифференцированность системы и производное состояние оперативной подсистемы по отношению к консервативной.

Третий этап диморфоза характеризуется асинхронным развитием дифференцированных подсистем в одну сторону, что объясняется включением в процесс управления консервативной подсистемы. Обозначение данного этапа на формуле: X' + Y'.

На четвёртом этапе диморфоза управляющая информация уже вновь отсутствует и происходит конвергенция (схождение) дифференцированных подсистем за счёт того, что развитие оперативной подсистемы приостанавливается, а консервативная “дотягивается” к её текущему состоянию. На формуле: X' + Y.

В окрестности переходного мгновения между четвёртым и пятым этапами дифорфоза дифференцированность подсистем перестаёт наблюдаться, а система принимает слитную форму S', производную от начальной S.

Как по формулам, так и по графической схеме заметно, что нормальный диморфоз при условии ненарушения причинно-следственных отношений является необратимым процессом.

Диморфологические гипотезы об относительности

1. Более количественно интенсивное развитие отдельного свойства объекта сопровождается и более выразительными диморфологическими явлениями данного свойства.

2. Чем выше производный коэффициент диморфологической метрики объекта относительно тождественной метрики другого объекта, гомологичного данному, тем выше и наблюдаемая скорость развития такого объекта по соответствующему показателю.

Математические замечания

Диморфологический предмет по содержанию инвариантен относительно природы исследуемых явлений, следовательно, он является математическим объектом и может быть описан средствами дискретной (конечной) математики.

Дискретная морфология принципиально отличается от математической морфологии по научному объекту. В рамках последней исследуются математические сущности, которые не являются динамическими системами и не подчиняются законам физического мира.

Правильная диморфологическая модель научного объекта не может основываться на софистике, а неотъемлемо содержит формальное определение топологической структуры, которое соотносит абстрактную математическую формулировку понятий окрестности, предела и непрерывности с категориями предметной области.

Попытки некоторых исследователей применить методы комбинаторики к формально неправильным моделям, элементы которых не обладают свойством диффеоморфизма (взаимно однозначного и гладкого отображения), содержат фундаментальную ошибку, поскольку, согласно принципам общей топологии [Александров П. С. Введение в теорию множеств и общую топологию], диффеоморфными могут быть только многообразия одинаковой размерности.